linked list
Before we start we need to know pointer and array first.
Pointer
In computer science, a pointer is a programming language object, whose value refers to (or “points to”) another value stored elsewhere in the computer memory using its memory address.
& is the address operator
* is the dereferencing operator
Pointers are frequently used in C, as they have a number of useful applications. Such as:
–Used to pass information back and forth between a function and its reference point.
–Enable the programmers to return multiple data items from a function via function arguments or to pass arrays and strings as function arguments
–Provide an alternate way to access the individual elements of an array
–Used to create complex data structures, such as trees, linked list, linked stack, linked queue and graphs
–Used for the dynamic memory allocation of a variable
example in c:
int * pnum;
int x;
pnum = &x;
Array
Array is a linear list is an elementary abstract data type that allows storage of elements of the same data type in the same contiguous memory area.
•A collection of similar data elements
•These data elements have the same data type (homogenous) •The elements of the array are stored in consecutive memory locations and are referenced by an index
•Array index starts from zero
•Declaration: •int arr[5]; •
•Accessing: •arr[0] = 7;
•arr[1] = 2;
•arr[2] = 13;
•arr[3] = 13;
•arr[4] = 13;
Linked list
•Linked list is a data structure that consists of a sequence of data records such that each record there is a field that contains a reference to the next record in the sequence.
•Linked list allows insertion and deletion of any element at any location.
•Linked list is used in many algorithms for solving real-time problems, when the number of elements to be stored is unpredictable and also during sequential access of elements.
•A linked list consists of two types: –Single Linked List –Double Linked List
Array: Linear collection of data elements, Store value in consecutive memory locations, Can be random in accessing of data •
Linked List: Linear collection of nodes, Doesn’t store its nodes in consecutive memory locations, Can be accessed only in a sequential manner
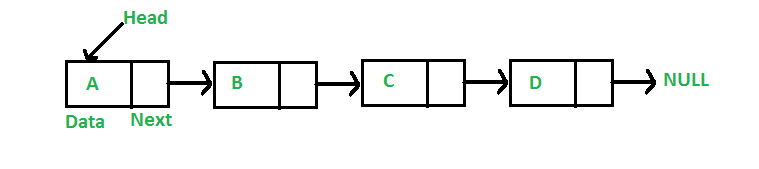
Single Linked List
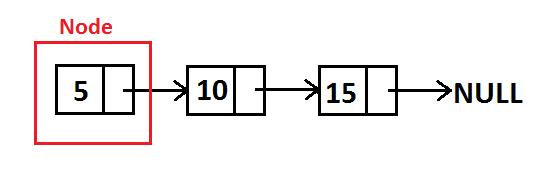
Single linked list: Delete Algorithm
•To delete a value, first we should find the location of node which store the value we want to delete, remove it, and connect the remaining linked list.
• •Supposed the value we want to remove is x and assuming x is exist in linked list and it is unique. •
•There are two conditions we should pay attention to: if x is in a head node or, if x is not in a head node.
Double Linked List
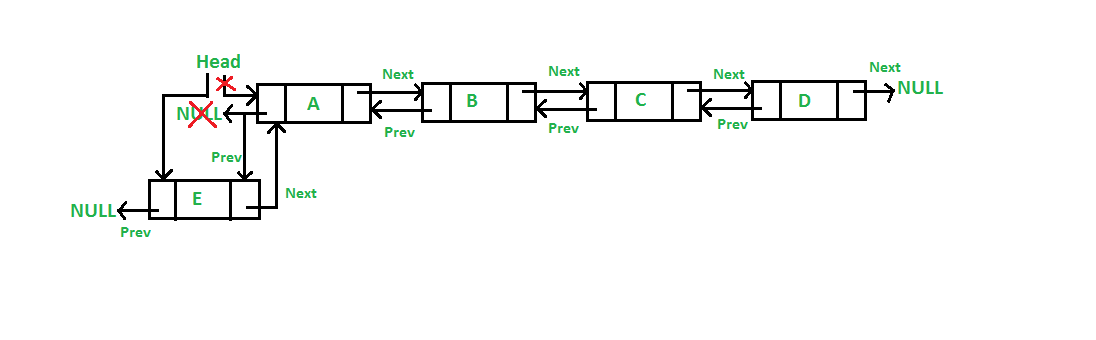
Picture above is the visual of double linked list.
A Doubly Linked List (DLL) contains an extra pointer, typically called previous pointer, together with next pointer and data which are there in singly linked list.
Advantages over singly linked list
1) A DLL can be traversed in both forward and backward direction.
2) The delete operation in DLL is more efficient if pointer to the node to be deleted is given.
3) We can quickly insert a new node before a given node.
In singly linked list, to delete a node, pointer to the previous node is needed. To get this previous node, sometimes the list is traversed. In DLL, we can get the previous node using previous pointer.
Hashing Table
Hashing is a technique that is used to uniquely identify a specific object from a group of similar objects. Some examples of how hashing is used in our lives include:
- In universities, each student is assigned a unique roll number that can be used to retrieve information about them.
- In libraries, each book is assigned a unique number that can be used to determine information about the book, such as its exact position in the library or the users it has been issued to etc.

In hashing, large keys are converted into small keys by using hash functions. The values are then stored in a data structure called hash table. The idea of hashing is to distribute entries (key/value pairs) uniformly across an array. Each element is assigned a key (converted key). By using that key you can access the element in O(1) time. Using the key, the algorithm (hash function) computes an index that suggests where an entry can be found or inserted.
Hashing is implemented in two steps:
- An element is converted into an integer by using a hash function. This element can be used as an index to store the original element, which falls into the hash table.
- The element is stored in the hash table where it can be quickly retrieved using hashed key.hash = hashfunc(key)
index = hash % array_size
•Hashing is a technique used for storing and retrieving keys in a rapid manner.
•In hashing, a string of characters are transformed into a usually shorter length value or key that represents the original string.
•Hashing is used to index and retrieve items in a database because it is faster to find item using shorter hashed key than to find it using the original value.
•Hashing can also be defined as a concept of distributing keys in an array called a hash table using a predetermined function called hash function.
•Hash table is a table (array) where we store the original string. Index of the table is the hashed key while the value is the original string.
•The size of hash table is usually several orders of magnitude lower than the total number of possible string, so several string might have a same hashed-key.

Picture above is a example of hash table.
A hash function is a mathematical function that converts a numerical input value into another compressed numerical value.
•There are many ways to hash a string into a key. The following are some of the important methods for constructing hash functions.
•Mid-square
•Division (most common)
•Folding
•Digit Extraction
•Rotating Hash
Mid Square
algorithm:
- Choose a seed value. This is an important step as for same seed value, the same sequence of random numbers is generated.
- Take the square of the seed value and update seed by a certain number of digits that occur in the square. Note: The larger is the number of digits, larger will be the randomness.
- Return the key.
Stack & Queue
•Stack is an important data structure which stores its elements in an ordered manner •Analogy:
You must have seen a pile of plates where one plate is placed on top of another. When you want to remove a plate, you remove the topmost plate first. Hence, you can add and remove an element (i.e. the plate) only at/from one position which is the topmost position
•Stack is a linear data structure which can be implemented by either using an array or a linked list. •The elements in a stack are added and removed only from one end, which is called the top. •The data are stored in Last In First Out (LIFO) way. •
•Stack has two variables: vTOP which is used to store the address of the topmost element of the stack vMAX which is used to store the maximum number of elements that the stack can hold •If TOP = NULL, then indicates that the stack is empty •If TOP = MAX – 1, then the stack is full • • •TOP=4, insertion and deletion will be done at this position
•Technique of creating a stack using array is easier, but the drawback is that the array must be declared to have some fixed size. •In a linked stack, every node has two parts: vOne that stores data vOne that stores the address of the next node •The START pointer of the linked list is used as TOP •All insertions and deletions are done at the node pointed by the TOP •If TOP = NULL, then it indicates that the stack is empty
•push(x) : add an item x to the top of the stack. •pop() : remove an item from the top of the stack. •top() : reveal/return the top item from the stack. • • •Note: top is also known as peek.
•Queue can be implemented by either using arrays or linked lists. •The elements in a queue are added at one end called the rear and removed from the other one end called front. •The data are stored in First In First Out (FIFO) way, this is the main difference between stack and queue. •
•Similar with stack, technique of creating a queue using array is easy, but its drawback is that the array must be declared to have some fixed size. •In a linked queue, every element has two parts –One that stores the data –Another that stores the address of the next element •The START pointer of the linked list is used as the FRONT •All insertions will be done at the REAR, and all the deletions are done at the FRONT end. •If FRONT = REAR = NULL, then it indicates that the queue is empty
•push(x) : add an item x to the back of the queue. •pop() : remove an item from the front of the queue. •front() : reveal/return the most front item from the queue. •
front is also known as peek. •
•Using the previous implementation, what will happen if we push MAXN times and pop MAXN times, and we try to push another data into the queue? • •Yes, we can not do that. The R index will overflow (exceeding MAXN), which means the new data will be stored outside the array range. • •It seems very inefficient, how to deal with this?
Binary Search Tree
•Binary Search Tree (BST) is one such data structures that supports faster searching, rapid sorting, and easy insertion and deletion •BST is also known as sorted versions of binary tree •For a node x in of a BST T, –the left subtree of x contains elements that are smaller than those stored in x, –the right subtree of x contains all elements that are greater than those stored in x,
with the assumptions that the keys are disti
•Binary Search Tree has the following basic operations: vfind(x) : find key x in the BST vinsert(x) : insert new key x into BST vremove(x) : remove key x from BST
•Because of the property of BST, finding/searching in BST is easy. • •Let the key that we want to search is X. vWe begin at root vIf the root contains X then search terminates successfully. vIf X is less than root’s key then search recursively on left sub tree, otherwise search recursively on right sub tree.
•Inserting into BST is done recursively. • •Let the new node’s key be X, vBegin at root vIf X is less than node’s key then insert X into left sub tree, otherwise insert X into right sub tree vRepeat until we found an empty node to put X (X will always be a new leaf) • •
•There are 3 cases which should be considered: vIf the key is in a leaf, just delete that node vIf the key is in a node which has one child, delete that node and connect its child to its parent vIf the key is in a node which has two children, find the right most child of its left sub tree (node P), replace its key with P’s key and remove P recursively. (or alternately you can choose the left most child of its right sub tree) • •
